Handling Decimals in Hardware: A Closer Look 🧐

This post talks about how the decimal numbers are actually stored in the memory.

So how are the decimals stored?

There are two different types of notations to store decimal numbers in the memory. The first one is floating-point notation, and the other is fixed-point notation.

Let's start with floating-point notation!

Consider a floating-point number 10.75. Let’s go step by step and understand how 10.75 is actually stored in the memory.

Step 1: Convert floating-point number to binary format

In 10.75 , the integral part is 10 and the decimal part is 0.75.

The binary representation of 10 would be 1010. To get the binary representation of 0.75 we need to follow these steps:  

0.75 * 2 = 1.50      // Take 1 form this and move 0.50 to the next step.

0.50 * 2 = 1.00    // Take 1 and stop here, since there is no remainder.

Ever wonder, why we need to multiply the decimal/fractional part with 2 and take out 1/0, to convert it to equivalent binary?

To understand this we need to understand how the fractional numbers are represented in binary number system. Let’s take a fractional number in binary as abc.pqr, now to convert this to decimal, we do:

(a x 2^2) + (b x 2^1) + (c x 2^0) . (p x 2^-1) + (q x 2^-2) + (r x 2^-3)

From the above expression, it is clear that we are summing up the decimal part by multiplying it with 2^-n to convert from binary to decimal. Similarly, when we do the backward process (converting from decimal to binary), we multiple the decimal part with 2, which is easier than dividing by 1/2^n and then finding out the remainder every time.

The reason behind taking 1 or 0 out every time we multiply the decimal number with 2 is simple. This is because in binary, we have only two digits, 0 and 1. If the result of the multiplication is greater than or equal to 1, we know that the power of 2 corresponding to that position contributes to the decimal fraction, so we take 1. Otherwise, if the result is less than 1, we know that the power of 2 does not contribute to the decimal fraction, so we take 0.

Okay! now let us continue our calculation. 😀

The binary representation of 0.75 would be .11

Finally, the binary representation of the floating point number 10.75 would be 1010.11.

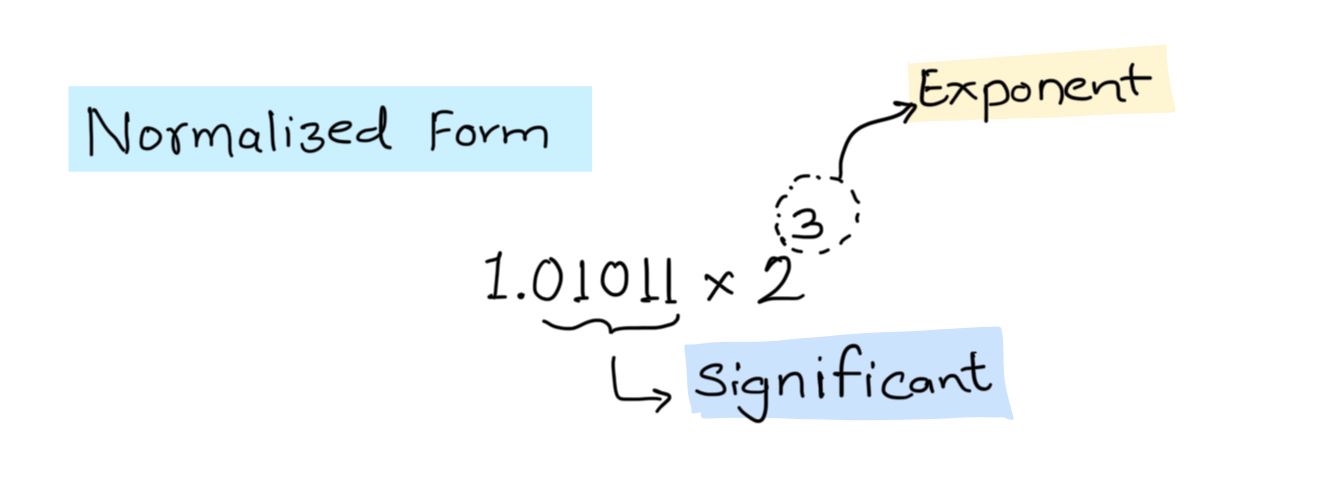
Step 2: Normalize the converted binary

The floating point number should be normalized into the format 1.significant*2^(exponent).

So, 1010.11 would be normalized as 1.01011 * 2^3 since we have shifted decimal to 3 bits left.

In the normalized value, the binary data after the decimal point is called significant, which is 01011.

Step 3 : Adding bias value

In floating-point numbers there is no concept of 2’s complement to handle negative numbers, so to manage this a bias addition was introduced. This bias value would be added whether the number is positive or negative, to reduce the complexity. 

Bias(n) = 2^(n-1)-1

Here n corresponds to number of bits allocated for exponent in the floating point number storage. 

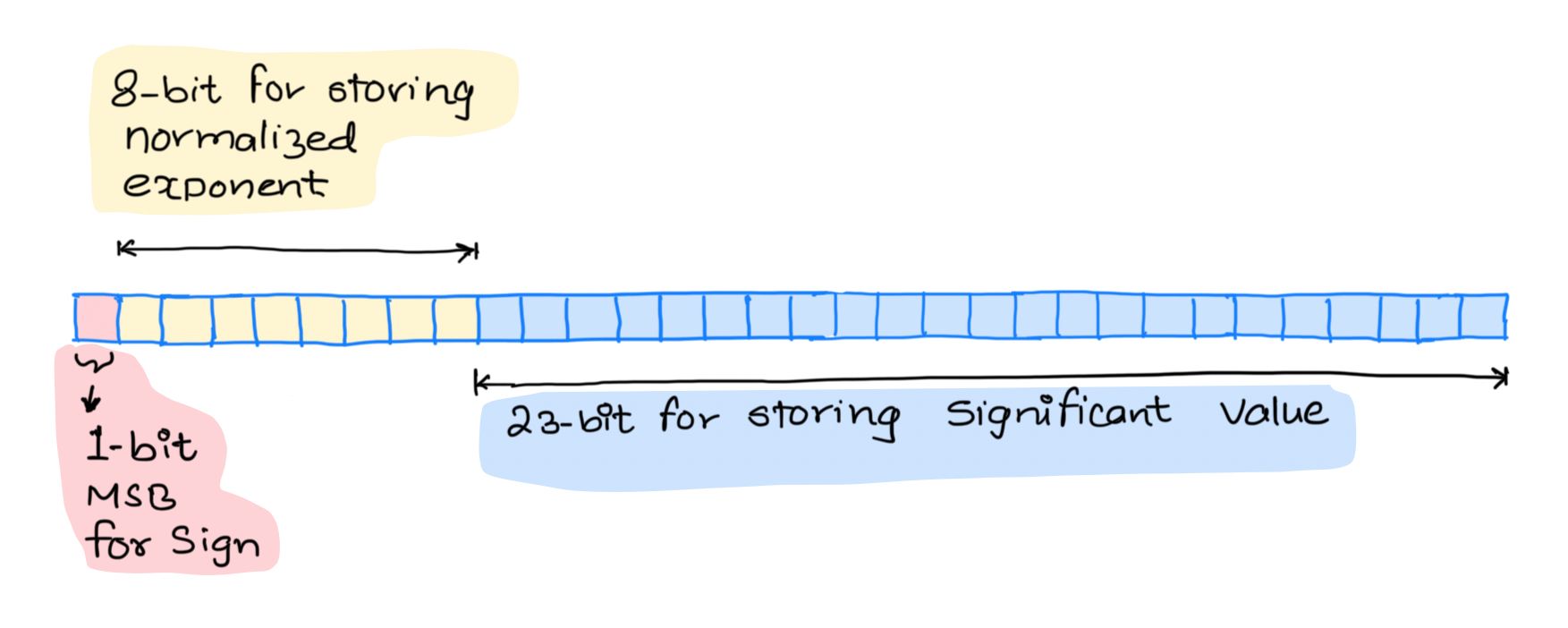
Note: For a floating point number 4-bytes (32-bits) are allocated in total to store sign, mantissa and exponent data. Out of which 1-bit is allocated to sign information, 8-bits are allocated for normalized exponent and 23-bits are allocated to store significant. 

Whereas to store double 8-bytes (64-bits) of memory is allocated, where 1-bit is allocated for sign, 11-bits for exponent and 52-bits for storing significant.

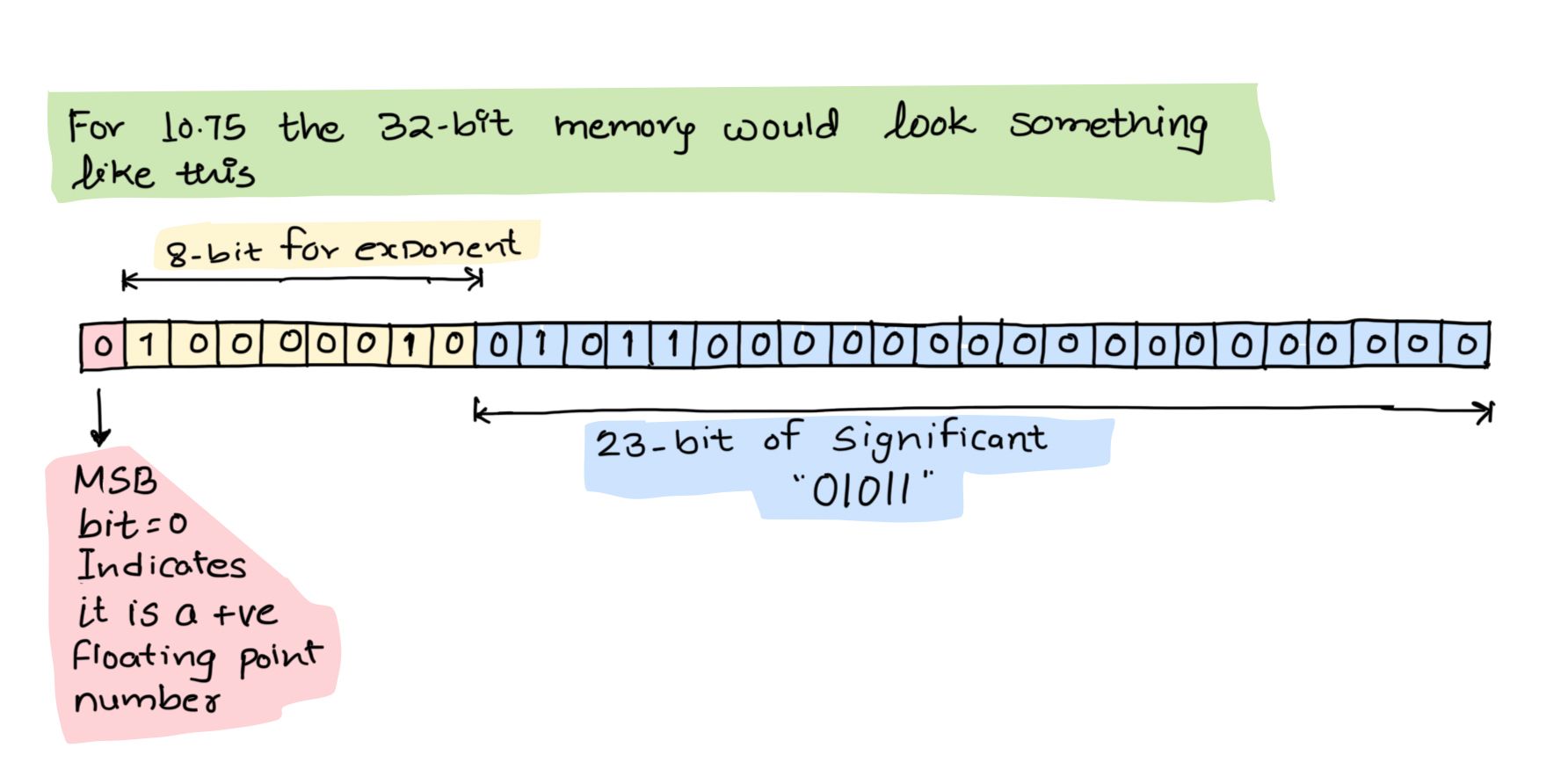
Since we are talking about floating point number here, 8-bits are allocated for exponent, the Bias(8) would be 127. This bias value is added to the exponent to get the normalized exponent value, which would be 3 + 127 = 130.

Binary form of 130 is 10000010

Step 4: Storing sign, exponent and significant to memory

We have sign bit as 0, the normalized exponent value as 10000010 and significant value as 01011.

Fixed-Point numbers representation in memory!

Now let us talk about another way of storing decimal numbers in the hardware. This way of representing decimal numbers has fixed number of bits allocated for integer part and for decimal/fraction part.

For example, let’s consider that the standard format allocated to you is IIII.FFFF, then the minimum value that you could store is 0000.0001 and the maximum value that you could store is 9999.9999. Since we now got some introduction about fixed-point representation, let’s delve more into it.

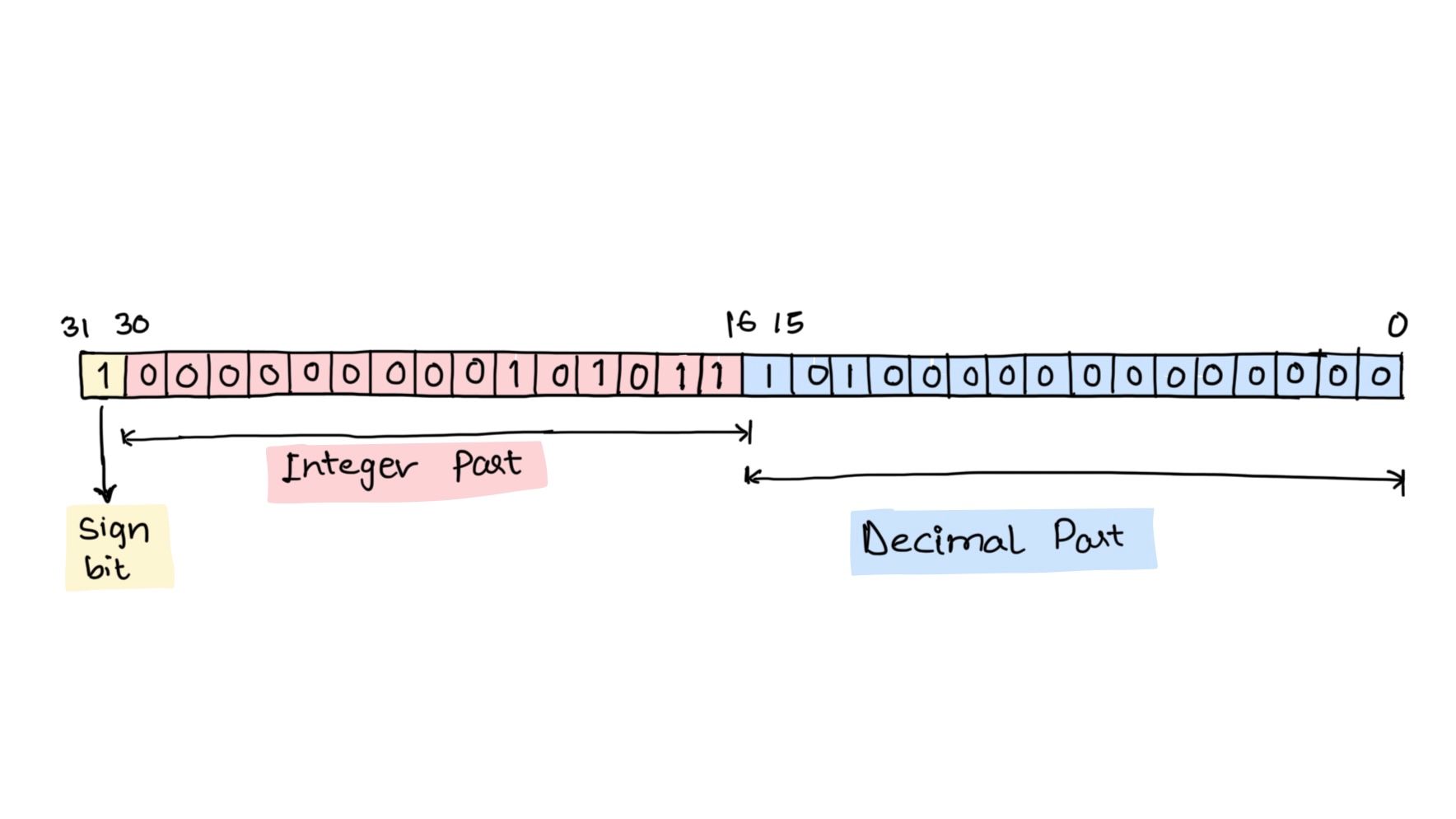
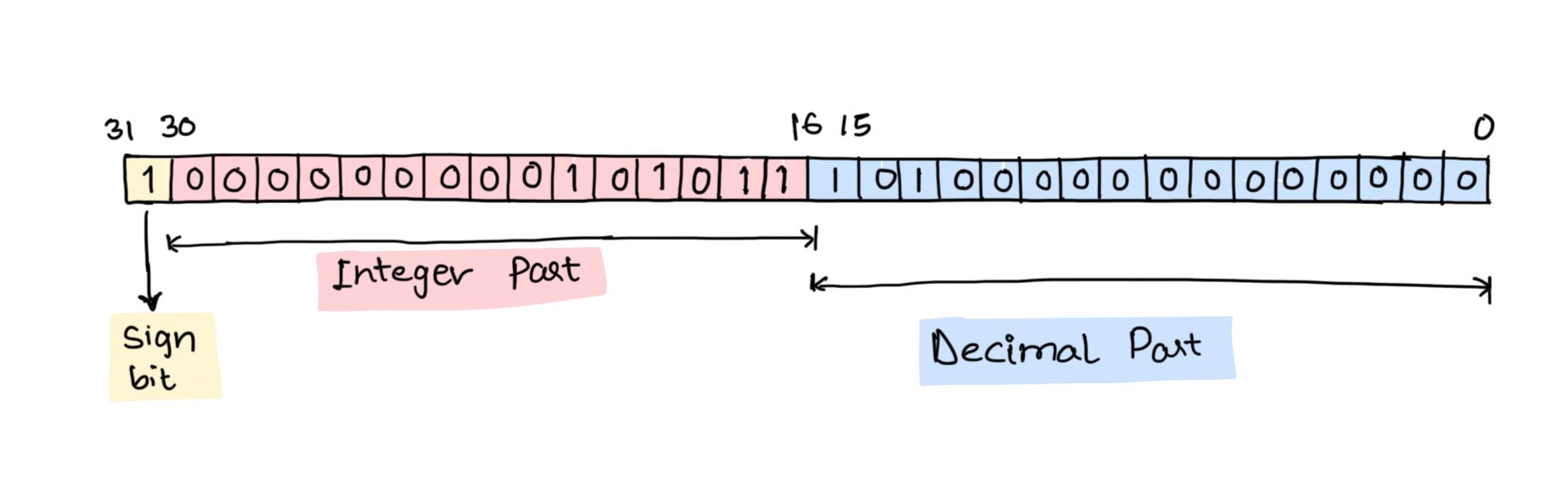
The fixed-point representation of decimal numbers is divided into 3 parts, the first one being the SIGN BIT, the second being the INTEGER PART and the third one is the DECIMAL or FRACTIONAL PART. Assuming that 32-bit format is used, in this case, 1-bit is allocated to SIGN BIT, 15-bits are allocated for INTEGER PART and 16-bits are allocated for DECIMAL or FRACTIONAL PART.

Let’s consider the decimal number -43.625 and apply fixed-point!

Let’s break -43.625 into three parts, the SIGN BIT which would be 1 since it is a negative number, the INTEGER PART, which is 43 (binary = 101011) and the DECIMAL or FRACTIONAL PART which is 0.625 (using the above binary conversion process, the binary would be 1010000000000000). So the 32-bit memory would be filled with these values : 

SIGN BIT- 1 (1-bit)
INTEGER PART- 000000000101011 (15-bits)
DECIMAL or FRACTIONAL PART- 1010000000000000 (16-bits)

Okay, is fixed-point better or floating-point?

Since we have known about both the methods of representing decimal numbers in the memory, the question comes on when to use what?

When is fixed-point representation useful?

The fixed-point notation is useful when we have limited resources, known range requirements, and need predictable behaviour. It is useful in low-end embedded systems, real-time processing, and applications where resources are constrained.

When is floating-point representation useful?

The floating-point representation is useful when a wide dynamic range and high precision is required. Especially in scientific and engineering computations, simulations, and applications dealing with real numbers.

Summing up, the choice between fixed-point and floating-point notation depends on the specific needs of the application. Both the notations have their pros and cons, so understanding the requirements and properties of each notation will help in making an informed decision!

Hope you loved this post! This was contributed by one of the community members: Zahid Basha S K! 🙌