Why 2’s complement makes sense?
When the negative numbers are encoded using two’s complement encoding, it has similar trait as positive numbers. This property makes it possible to reuse the same hardware between positive and negative numbers. Hence the two’s complement makes sense for hardware design perspective.

Background
What is the 8-bit binary representation of the number +3? Well, it’s simple 00000011. and what is the 8-bit binary representation of the number -3? We know that the negative numbers use the MSB for sign bit, so intuitively one might guess that -3 is represented as 10000011 but that’s not correct.
Computer systems represent the negative numbers in the 2’s complement format. That means -3 is represented as 11111101. Why did they choose 2’s complement instead of simple 1’s complement? In this post, we will discuss why this choice was made.
Number format choice
Let us take a smaller example with 4-bit numbers. unsigned 4-bit number can hold values from 0 to 15. While signed 5-bit number uses MSB for encoding and remaining bits represent the magnitude of the number. There are two options:
- 1’s complement format - Magnitude for the positive and negative numbers are same. MSB bit describes the sign. (+3 is
00000011and -3 is10000011) - 2’s complement format - To get a negative number, we invert all the bits from positive number and add
1to it. (+3 is00000011and -3 is11111101)
Following diagram describes how the encoding for 1’s complement and 2’s complement format looks like for 4-bit Numbers.
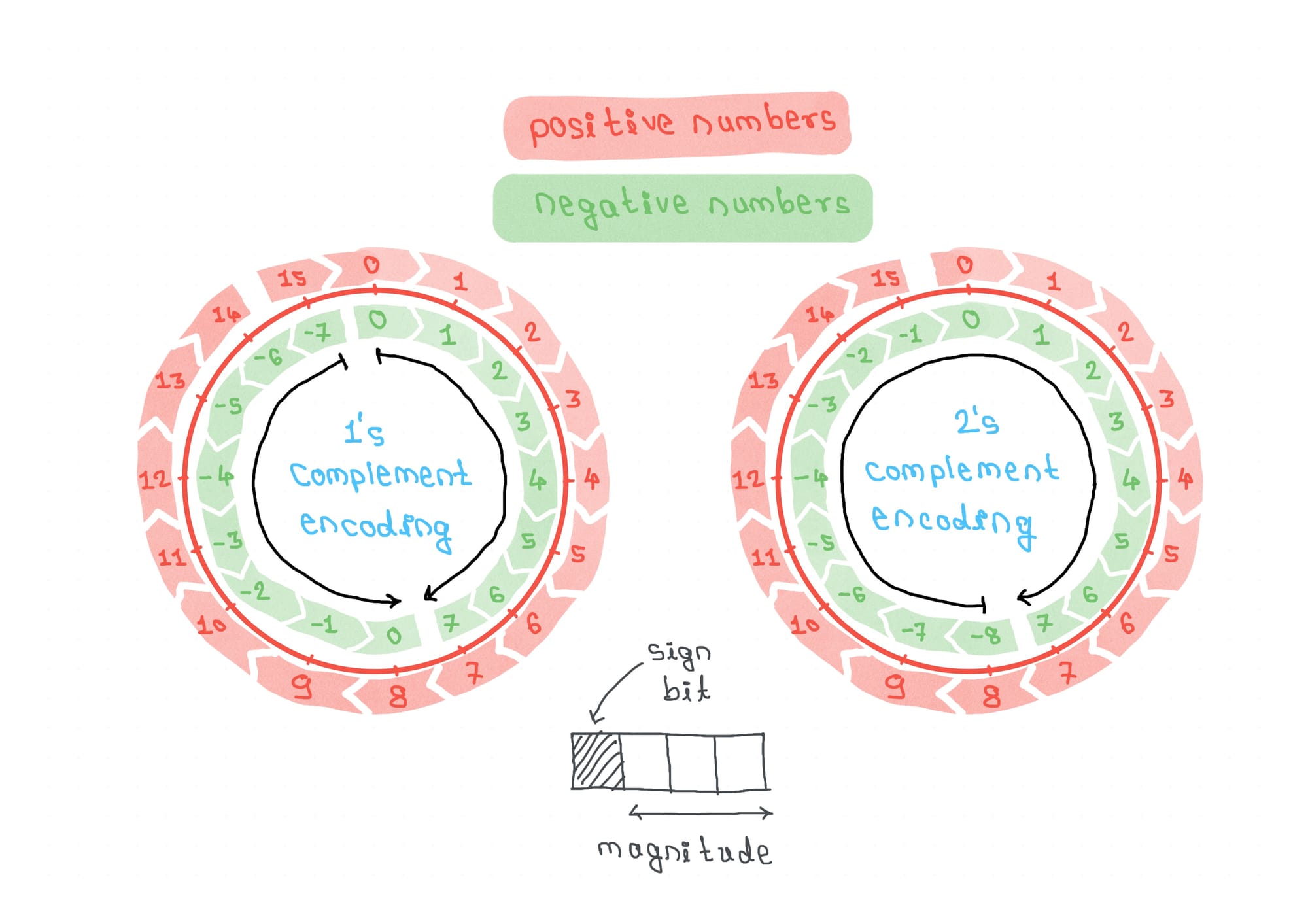
In this diagram, we describe how the same bit pattern is used to encode 4-bit unsigned and 4-bit signed numbers for different encoding schemes. One thing to note here is that for 1’s complement format (left), the numbers are not always increasing in clock-wise direction. But in the case of 2’s complement format(right), the numbers are always increasing in clock-wise direction.
ALU likes 2’s complement
In a computers, the ALU is a hardware responsible for doing various arithmetic operations like addition, subtraction, multiplication, etc.
Imagine a hardware that does simple arithmetic calculations on the unsigned numbers. Here 10 + 2 would require us to start from 10 and move two blocks in the clock-wise direction. Similarly, 10 - 3 would require us to start from 10 and move three blocks in any clock-wise direction.
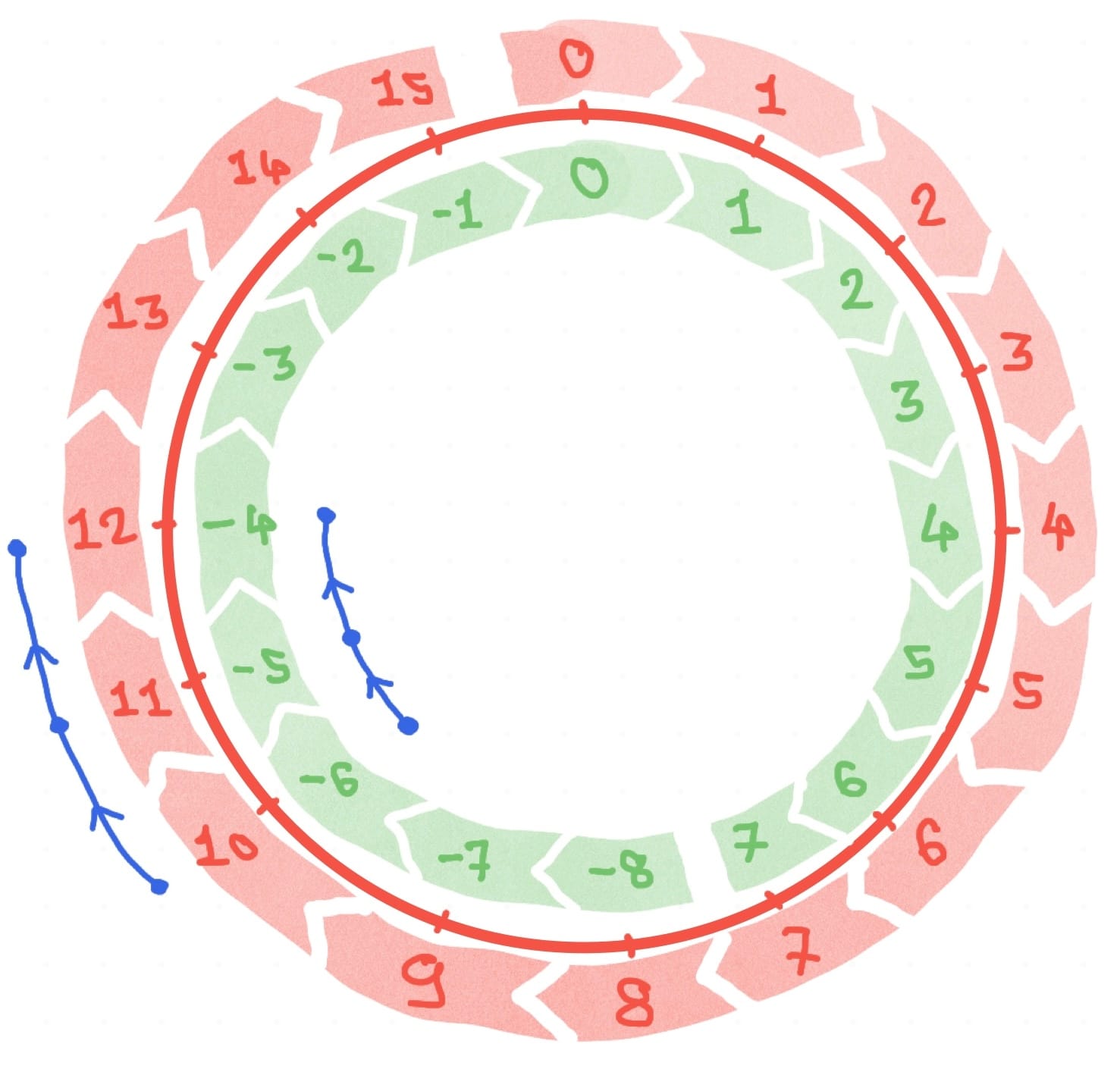
If we try to apply similar analogy for 1’s complement encoding, it does not work since the numbers are not either increasing or decreasing. So we need a different and more complex hardware for handling the negative numbers 😦
Now let’s look at 2’s complement encoding. It shares the same trait as unsigned numbers. All numbers are increasing in clock-wise direction. e.g. adding 2 to a number would just mean jumping 2 blocks clockwise and subtracting 3 would mean jumping 3 numbers reverse direction. This means the ALU can simply reuse the hardware for unsigned numbers to do arithmetic on 2’s complement signed numbers.
Go ahead and try it yourself. Take two signed numbers, then decide to add or subtract them. Perform all the arithmetic using the corresponding unsigned numbers and you will still get correct result.
e.g. When we want to do-6 + 2, we do the addition of the corresponding unsigned numbers10and2. (answer =12) and interpret the result as signed number, we get correct answer-4.
Hardware block reuse
By choosing the 2’s complement format, the computer system hardware can be designed efficiently and the same hardware blocks can be used mostly for handling unsigned as well as signed numbers. In fact, when you check the assembly level, the instructions to add 2 unsigned numbers and instructions to add 2 signed numbers are exactly the same. That’s because hardware does not really care about it. It does exactly the same thing for both signed vs unsigned variables.
Ease of conversion
Another benefit of 2’s complement encoding comes from the ease with which we can typecast from 8-bit to 16-bit and vice versa. A simple sign extension logic (where the MSB bit is copied into all the new bits) is used to extend a number from smaller bit width to higher bit width As shown below.
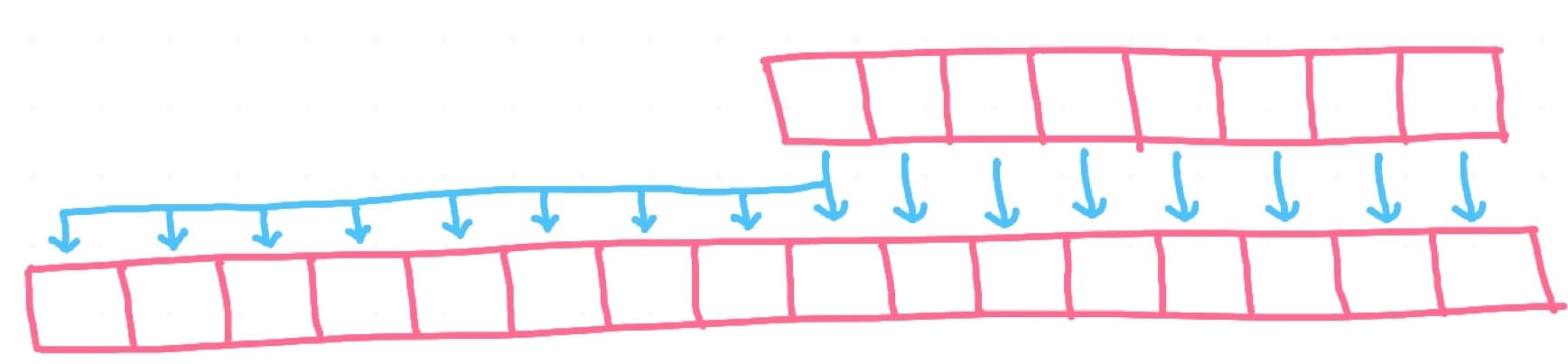
If we had used 1’s complement format, the same operation gets complicated when we have to support type casting between different bit widths like 8-bit, 16-bit, 32-bit, etc.
What’s the catch?
2’s complement encoding simplifies the ALU hardware design for most part. Except the negation, that involves a bit inversion and an addition with 0x1. It adds some confusion for humans to interpret the negative numbers. Also, this format does not cover the positive and negative range equally. There will Always be one extra negative number that can be represented by this encoding. e.g. 8-bit numbers will cover the range -128 to +127.
The benefits outweigh the disadvantages that all it makes sense to use 2’s complement everywhere.
Conclusion
- Use of 2’s complement makes it easy for hardware designers to support negative numbers.
- Most of the hardware blocks in ALU can be reused to work with signed and unsigned numbers
- It provides consistent mechanism to perform type-casting across different bit widths

Discussion