0.1 is not 0.1. Yups!
C-language
0.1 is not 0.1. Yups!
Computers can't store 0.1 accurately. It is stored as 0.1000000015! In this post we explore and take a look at what is really going on.
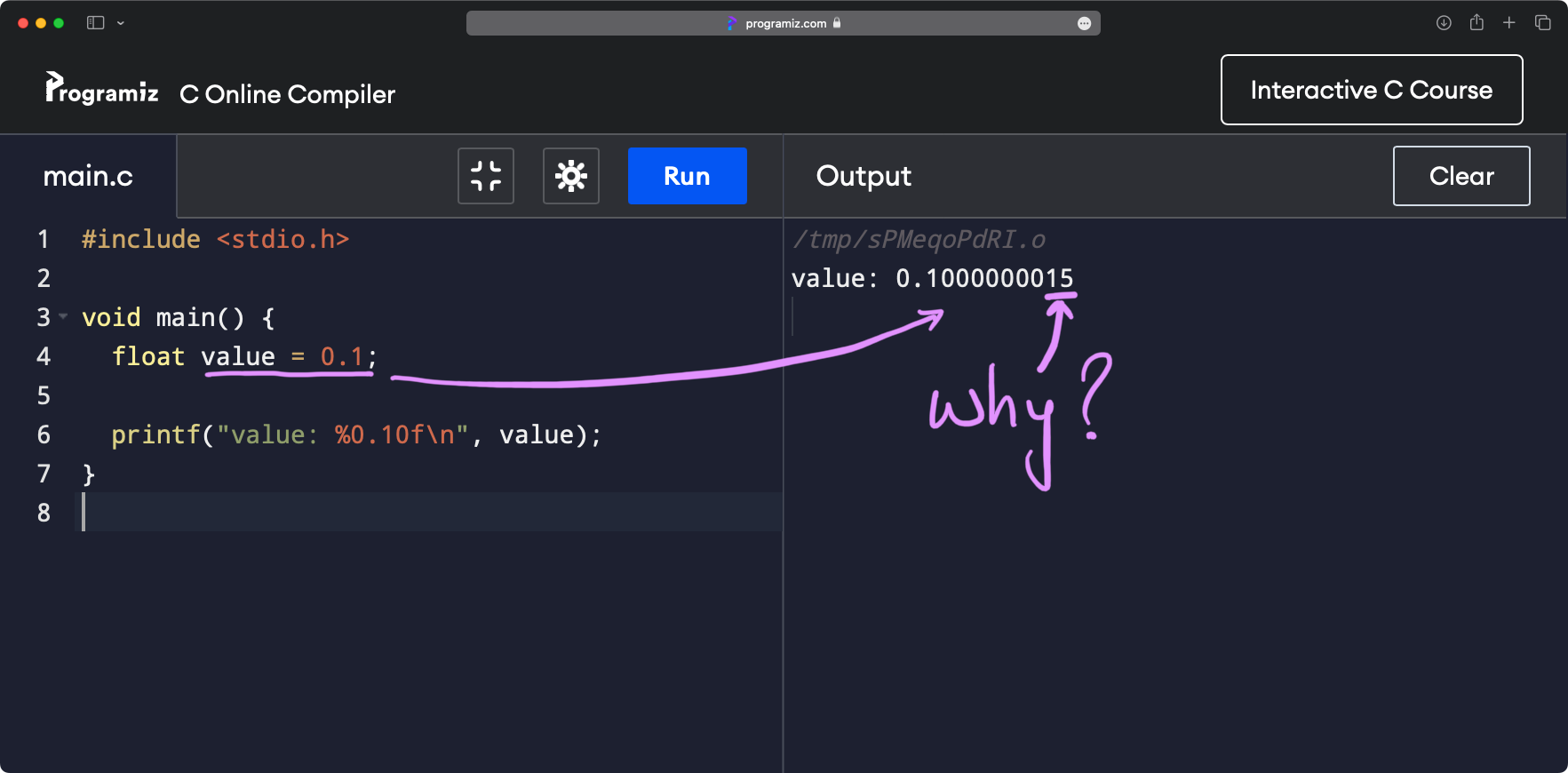
Computers can't store 0.1 accurately. It is stored as 0.1000000015! In this post we explore and take a look at what is really going on.

Helping you navigate the Embedded Systems career with ease! Technical posts, newsletters, special offers, and more.
Subscribe for Free!